Πώς ένα απλό μαθηματικό πρόβλημα θα είχε αποτρέψει τη «ληστεία του αιώνα» στην καρδιά των Παρισίων
Νωπές είναι ακόμη οι μνήμες από τη ληστεία στο Λούβρο όπου ομάδα ληστών κατάφερε να περάσει στην αίθουσα του Απόλλωνα και να αποσπάσει κοσμήματα αξίως 88 εκατομμυρίων ευρώ. Ωστόσο, ένας μαθηματικός γρίφος που μελετάται εδώ και μισό αιώνα ίσως να προσφέρει πολύτιμα διδάγματα για την προστασία των μουσείων.
Η ληστεία διήρκεσε μόλις οκτώ λεπτά. Σε αυτά τα 480 δευτερόλεπτα, οι δράστες ανέβηκαν σε μια μηχανική πλατφόρμα και έφτασαν σε ένα μπαλκόνι του πρώτου ορόφου του Λούβρου στο Παρίσι, πριν διαρρήξουν ένα παράθυρο υπό το φως της ημέρας. Μόλις μπήκαν, έσπασαν δύο γυάλινες προθήκες και διέφυγαν παίρνοντας μαζί τους οκτώ ανεκτίμητα κοσμήματα της εποχής του Ναπολέοντα.
Οι γαλλικές αρχές έχουν συλλάβει επτά υπόπτους. Η ερώτηση που απασχολεί τους ειδικούς αστυνομικούς και το κοινό είναι γιατί οι δράστες δεν εντοπίστηκαν νωρίτερα.
Η ομολογία της διευθύντριας
Κατά τη διάρκεια ακρόασης στη Γαλλική Γερουσία, η διευθύντρια του Λούβρου, Λοράνς ντε Κάρς, παραδέχτηκε ότι το μουσείο «απέτυχε να προστατεύσει» τα κοσμήματα της κορώνας.
Το μόνο κάμερα που κάλυπτε το μπαλκόνι, όπως αποδείχθηκε, ήταν στραμμένη προς τη λάθος κατεύθυνση, ενώ προκαταρκτική αναφορά έδειξε ότι ένα στα τρία δωμάτια της πτέρυγας Ντενόν δεν είχε καθόλου κάμερες. Η ίδια σημείωσε ότι οι περικοπές στην παρακολούθηση και το προσωπικό ασφαλείας είχαν αφήσει το μουσείο ευάλωτο και τόνισε ότι το σύστημα ασφαλείας πρέπει να ενισχυθεί για να «βλέπει παντού».
Παρά το γεγονός ότι οι συναγερμοί φέρεται να λειτούργησαν κανονικά, η ληστεία στο Λούβρο ήταν η τρίτη υψηλού προφίλ κλοπή από γαλλικά μουσεία μέσα σε δύο μήνες, οδηγώντας το Υπουργείο Πολιτισμού σε νέα σχέδια ασφάλειας.
Το μαθηματικό μυστικό πίσω από την ασφάλεια
Παρά τη σύγχρονη τεχνολογία, υπάρχει ένα μαθηματικό πρόβλημα ηλικίας 50 ετών που εξετάζει ακριβώς το θέμα αυτό: πόσους φύλακες ή κάμερες χρειάζεται για να καλύψουν ολόκληρο ένα μουσείο. Γνωστό ως «πρόβλημα του μουσείου» ή «πρόβλημα της γκαλερί τέχνης», η λύση του είναι ιδιαίτερα κομψή.
Το πρόβλημα υποθέτει ότι όλα τα δωμάτια έχουν ευθείες πλευρές, σχηματίζοντας πολύγωνα. Οι κάμερες, τοποθετημένες σε σταθερά σημεία, μπορούν να βλέπουν σε όλες τις κατευθύνσεις. Για πλήρη κάλυψη, κάθε σημείο του δωματίου πρέπει να είναι ορατό από τουλάχιστον μία κάμερα.
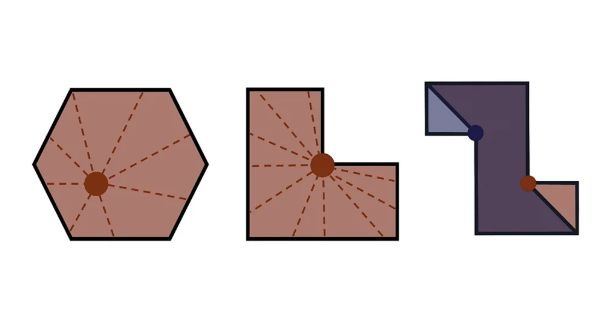
Σε ένα απλό εξάγωνο δωμάτιο, οποιαδήποτε τοποθέτηση μιας κάμερας μπορεί να καλύψει όλο το χώρο. Σε ένα L-σχήματος δωμάτιο, η κάμερα πρέπει να τοποθετηθεί στρατηγικά. Και σε πιο περίπλοκα σχήματα, όπως ένα Z-σχήμα, χρειάζονται τουλάχιστον δύο κάμερες.
Η λύση του Václav Chvátal και η απόδειξη του Steve Fisk
Το 1973, ο Ούγγρος θεωρητικός γραφημάτων Václav Chvátal έλυσε το πρόβλημα σε γενικούς όρους. Η βασική ιδέα είναι ότι ο αριθμός των γωνιών ενός δωματίου διαιρείται με το τρία για να δώσει τον αριθμό των καμερών που χρειάζονται για πλήρη κάλυψη. Για παράδειγμα, ένα δωμάτιο με 15 γωνίες απαιτεί πέντε κάμερες, ενώ ένα με 20 γωνίες χρειάζεται έξι.

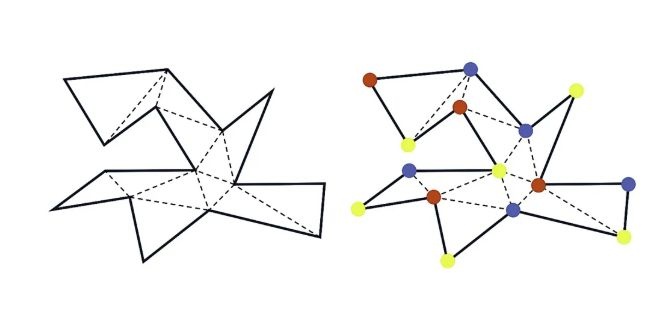
Πέντε χρόνια αργότερα, ο Steve Fisk ανέπτυξε μια εντυπωσιακή απόδειξη, χρησιμοποιώντας τριγωνοποίηση και «τριχρωματισμό». Κάθε τρίγωνο στο δωμάτιο έχει τρεις γωνίες διαφορετικού χρώματος. Επιλέγοντας το χρώμα με τις λιγότερες γωνίες, οι κάμερες που τοποθετούνται εκεί μπορούν να καλύψουν ολόκληρο το δωμάτιο. Το αποτέλεσμα είναι ότι ακόμη και πολύπλοκα σχήματα μπορούν να προστατευτούν με λίγες στρατηγικά τοποθετημένες κάμερες.
Ευτυχώς για τα παραδοσιακά μουσεία με κυρίως ορθογώνια δωμάτια, μια παραλλαγή του προβλήματος δείχνει ότι αρκεί μία κάμερα για πλήρη κάλυψη. Αντίστοιχα, οι παραλλαγές γνωστές ως «πρόβλημα φρουράς» ή «πρόβλημα φυλακής» εξετάζουν την εξωτερική περίμετρο των κτιρίων, λύνοντας ζητήματα όπως η παραβίαση των εξωτερικών τειχών, που ήταν πρόβλημα και στο Λούβρο.
Οι κλέφτες που εισέρχονται μέσω δημόσιων εκθέσεων δεν είναι η μόνη απειλή. Το Βρετανικό Μουσείο, για παράδειγμα, είδε ένα δαχτυλίδι Cartier αξίας 760.000 λιρών να εξαφανίζεται το 2011, ενώ λίγα χρόνια αργότερα εμφανίστηκε προς πώληση στο eBay, φέροντας την υπογραφή εσωτερικής κλοπής από υπάλληλο.
Εκτός από τις κλοπές, τα μουσεία πρέπει να προστατεύουν τα έργα τους από βανδαλισμούς, πυρκαγιές και άλλες μορφές καταστροφής.
Μαθηματικά σε δράση πέρα από τα μουσεία
Το «πρόβλημα της γκαλερί τέχνης» βρίσκει εφαρμογές και σε άλλους τομείς. Στη ρομποτική βοηθά στον καλύτερο προγραμματισμό διαδρομών και την αποφυγή συγκρούσεων.
Στην πολεοδομία καθοδηγεί την τοποθέτηση κεραιών, σταθμών κινητής τηλεφωνίας και αισθητήρων ρύπανσης. Στην αντιμετώπιση καταστροφών, χρησιμοποιείται για την τοποθέτηση drones ή ιατρικών σταθμών. Στην επεξεργασία εικόνας και την οπτική υπολογιστών, βοηθά στον εντοπισμό ορατών περιοχών και στον φωτισμό θεατρικών σκηνών.
Το Λούβρο δεν απάντησε σε ερωτήσεις σχετικά με το αν γνώριζε τη λύση που προσφέρει το πρόβλημα του μουσείου. Ωστόσο, καθώς μουσεία και γκαλερί σε όλο τον κόσμο επανεξετάζουν την ασφάλειά τους μετά τη ληστεία, δεν υπάρχει αμφιβολία ότι η σοφία αυτού του 50χρονου μαθηματικού γρίφου παραμένει πολύτιμη.
